Реферат: Реверсная магнитная фокусирующая система мощного многолучевого клистрона

которое решается при следующих начальных условиях:

Интегрирование производится до q2 = q2*, где q2* - решение уравнения (2.5) для данного x.

Соответствующее q2* значение переменной x есть x*, которая используется дня вычисления цилиндрических координат r и z:

В большинстве практических случаев уравнения (2.5) и (2.6), определяющие внешнюю задачу, могут быть решены лишь численно с помощью электронных вычислительных машин.

Распределение потенциала внутри пучка в первом приближении параксиальной теории формировании в криволинейной системе координат определяется уравнением

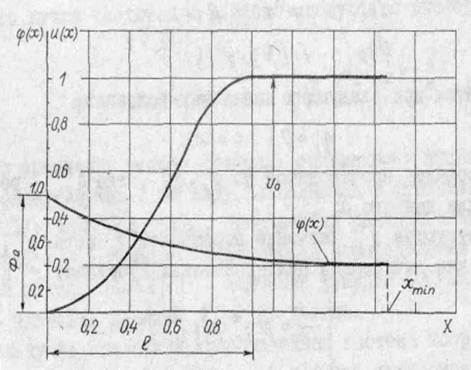
где V1 - потенциал искомой эквипотенциали. Распределение плотности тока внутри пучка в криволинейной системе координат является однородным.

Расчет электростатических электронных пушек.

Выберем за единицу измерения радиальных размеров системы формирования Ф0 начальный радиус пучка, а за единицу продольных размеров пушки l - расстояние от катода до точки пролетного канала, в которой потенциал на оси пучка достигает своего постоянного значения U0 (рис. 2.1). Величину U0 примем за единицу измерения потенциала.

При решении внутренней задачи для электростатической ЭОС имеются лишь две возможности: либо задаются траектории электронов в системе, а осевое распределение потенциала вычисляется из уравнения (2.2), либо, наоборот, задается распределение потенциала на оси системы, а из уравнения (2.2) вычисляются траектории электронов.

Как распределение потенциала [Функция и(х)], так и траектория электронов [функция f(x)] в электронной пушке должны подчинятьcя определенным условиям. Условия для функции и(х):

Условия (2.10) обеспечивают работу катода в режиме пространственного заряда, а условия (2.11) - отсутствие электрического поля на оси в заданном пространстве пушки.

Условие для функции j(x) при х=0:

Условие (2.12), как показано в теории формирования, обеспечивает сферичность эмитирующей поверхности катода.

Рассмотрим расчет пушки по принципу, когда задается функция и(х), а вычисляется функция j(x). В этом случае функцию и(х) можно задать так, чтобы условия (2.10), (2.11) выполнялись, но дополнительно нужно еще отыскать такой способ задания функции и(х) в области малых значений х, при котором функция j(x), вычисленная из уравнения (2.2), отвечала бы условию (2.12).

Если такой способ задания функции и(х) найден, то, проведя расчет нескольких вариантов решения внутренней задачи, можно выработать рекомендации по расчету электронных пушек, формирующих пучки с заданными параметрами.

Для решения уравнения (2.2) необходимо задать начальные условия. Решение внутренней задачи для электронной пушки удобнее проводить от катода, задавая значение функций и(х) и и'(х) при х = 0. Однако в этом случае на катоде и(х) = 0 и правая часть уравнения (2.2) обращается в бесконечность. Эту трудность можно обойти следующим образом. При заданной функции и(х) найдем приближенное аналитическое решение уравнения (2.2), справедливое в области малых х. При решении уравнения (2.2) с помощью полученного таким образом аналитического выражения сделаем первый шаг с катода в точку, в которой функция и(х) уже не равна нулю. Далее можно проводить решение уравнения (2.2) с помощью ЭВМ. Будем при расчете электростатической электронной пушки задавать функцию и(х) следующим выражением:

k, an (n = 1,2,…..5) – некоторые постоянные коэффициенты.

К расчету электронной пушки.

Риc. 2.1.

Очевидно, что функция и(х), заданная выражением (2.13), всегда положительна (при положительных х) и удовлетворяет условию (2.10). В области малых х функция и(х) совпадает о функцией kx4/3, описывающей распределение потенциала в плоском диоде.

Коэффициенты а1, а2, полинома (2.13) выберем таким образом, чтобы удовлетворялось условие (2.12), а с помощью коэффициентов а3, а4, a5 удовлетворим условию (2.11).

С целью отыскания соответствующих коэффициентов а1, а2, найдем для функции и(х), заданной выражением (2.13), приближенное решение уравнения (2.2), справедливое в области малых х.

При этом решение для функции j(х) будем искать в виде

Из этого выражения следует, что значение j"(x) при х = 0 определяется значением в2. Поэтому для выполнения условия (2.12) необходимо найти такие значения коэффициентов an, при которых в2 обращается в нуль. С этой целью подставим выражения (2.13), (2.15) в уравнение (2.2) и, приравнивая нулю коэффициенты при одинаковых степенях х, выразим вn через an. Расчет показывает, что вn выражается через коэффициенты а1, а2 и для выполнения условия в2= 0 эти коэффициенты должны вычисляться по следующим формулам:

Как следует и (2.15), коэффициент в1 определяет значение первой производной от функции j(x) в точке x = 0, т.е. на катоде. Поэтому введем обозначение в1 = j¢k, с учетом которого формулы (2.16) и (2.17) запишутся:

Этот расчет также показывает, что в области малых х коэффициенты к, в3, в4 связаны с постоянными коэффициентами i, а3, а4 следующими соотношениями:

С помощью этих соотношений можно вычислить приближенное решение уравнения (2.2), справедливое в области малых х, если значения коэффициентов а3, а4 известны.

Теперь вычислим такие значения коэффициентов а3, а4, а5, при которых удовлетворяются условия (2.11). Для этого возьмем первую и вторую производные от функции и(х) и в точке х = 1 положим u(1) = 1, u'(1) = 0, u"(1) = 0. Подучим систему трех уравнений, решая которую относительно а3, а4, а5, найдем:

Уравнения (2.13), (2.18), (2.19), (2.23) – (2.25) определяют способ задания функции и(х), при котором выполняются как условия (2.10), (2.11), налагаемые на функцию и(х), так и условие (2.12), налагаемое на функцию j (х).

После того как определена функция и(х), можно приступать к решению внутренней задачи для электростатической электронной пуша, т.е. к решению уравнения (2.2).

Будем решать уравнение (2.2) с помощью ЭВМ при следующих начальных условиях: х = х0; j = j0; j’ = j’0

Значение параметра х0 выберем малым (0,0001 + 0,01), а значения j0 и j’0 для точки х = х0 вычислим в соответствии с (2.15) по следующим формулам:

Значения коэффициентов в3, в4 в области малых х, должны вычисляться по формулам (2.21), (2.22), а входящие в них значения а3, а4, а5, определяются соотношениями (2.22) - (2.25).

Решение уравнения (2.2) c помощью ЭВМ будем проводить до точки xкр, в которой производная j’(х) обращается в нуль, т.е. до кроссовера пучка.

При решении внутренней задачи для электронной пушки необходимо задавать значения параметров i, j¢k. Параметр i, как следует из (2.4), характеризует первеанс рассматриваемой пушки. Параметр j¢k определяет радиус кривизны катода пушки (Rкp), который вычисляется по формуле:

Внешняя задача также решается с помощью ЭВМ. При этом с помощью уравнения (2.5) находится решение внешней задачи в криволинейной системе координат, а затем, решая уравнение (2.6), осуществляем переход к цилиндрической системе координат. При решении внешней задачи необходимо задавать параметр V = U / U0, где U - потенциал того электрода, форма которого вычисляется. При расчете геометрии прикатодного фокусирующего электрода значение параметра V полагается равным нулю, а при расчете формы анода пушки значение параметра V следует вычислять по формуле

где в = rn / rk - коэффициент заполнения канала пучком; rn, rk - соответственно радиусы пучка и пролетного канала.

Выражение (2.29) характеризует провисание потенциала в трубе дрейфа прибора, заполненной пучком с микропервеансом Рm и коэффициентом заполнения в. Оно следует из уравнений (2.2), (2.5) с учетом (2.11).

После решения внутренней и внешней задач по описанной выше методике необходимо с помощью (2.28) вычислить радиус кривизны катода Rкp. Радиус катода, характеризующий площадь его эмитирующей поверхности, определяется точкой пересечения дуги радиуса Rк с графиком функции j (х).

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9